The Machine Learning (ML) or Independent learning is a branch of Artificial Intelligence (AI) that aims to create systems that can learn by themselves from a set of data (data set), without being programmed explicitly
These systems can learn by themselves, a number of techniques and algorithms and are able to create predictive models, behavior patterns are etc. though this article is specific and limited to those techniques and algorithms that are part of the branch of ML list (there are some techniques that are clearly limited to this area), if we can say that in the area of ML fits all problem solving process, more or less explicitly based on a rigorous application of statistical decision theory; therefore, it is very normal that the ML area overlaps with the area of statistics. In ML unlike statistics, it focuses on the study of computational complexity of the problems, since most of these are of the NP-complete (or NP-hard) class and therefore the challenge of ML is to design workable solutions for such problems
Let’s look at two definitions of ML
Arthur Samuel (1959): The Machine Learning is a field of study that gives computers the ability to learn without being explicitly programmed.
Tom Michell (1998): A program is said to learn from experience ‘E’ with respect to any task ‘T’ and some measure of performance ‘R’ if their performance in ‘T’ measured by ‘R’ , improvement experience ‘E’
Learning System: Regression and Classification
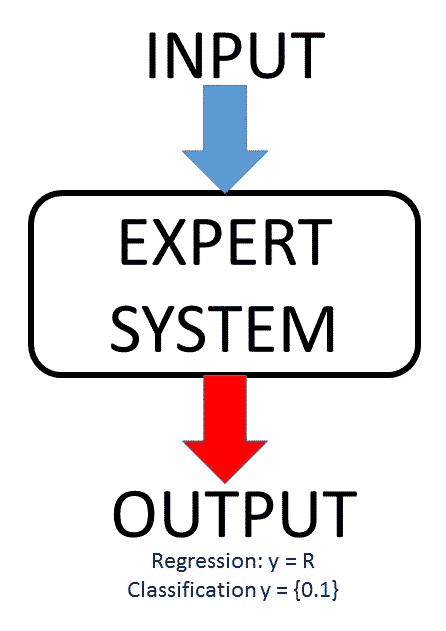
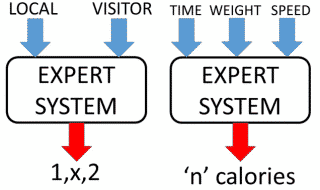
As mentioned in the definition of Machine Learning, this area must create systems that must be able to learn by themselves without being programmed explicitly for the purpose of predicting future events, make recommendations, classifications of items, events, tags, etc. So; after a learning phase, we will have an “expert system” for a given input we provide an output (prediction, recommendation, classification etc.) as a result of having applied a regression or classification function (which system must learn and apply) on the input data
Two examples of expert systems created after applying any technical ML , would be: one an expert system for predicting Cricket Matches (between Local and Visitor), which dropped the name of the local and visitor, computer returned as a result one of the three options of the Match (1, X, 2); and an another system expert in calculating calories burned (regression) to make continuous running (running), in which passing as input the weight of the person, race time and speed, return as a result the number of calories burned (0 <= calories <∞)
After explaining what is regression and classification, Lets see a more formal definition of the same:`
Regression: Both input data and output, belong to domains (X, Y) arbitrary. An example would be X = Y = R, with the resulting model or hypothesis a function
f: R → R
Classification: The input data X are arbitrary and exit Y is a finite set of N elements generally small Y = {1, 2, …, N}`
Lets see what kind of expert systems that get after applying any technical ML , we have to see how it learns and how this systems get that classification function or regression, which we will call “hypothesis.”
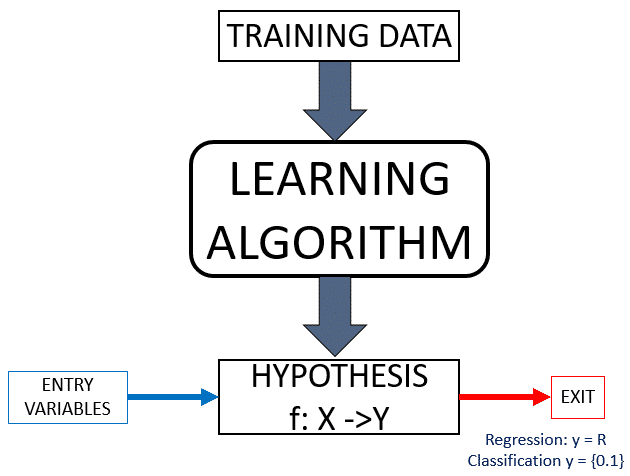
Systems to learn, must have a set of data (or data set) for learning or training (input and output) that are used to obtain a hypothesis (model or function) that generalizes the data properly. When it comes to “generalize” talking about predicting the output from new input data (test data) different from the training data.
This learning process for obtaining a hypothesis, we can see outlined in the following image. First we have a set of data that we use to train or teach the system. Applying some of the techniques of Machine Learning, get a hypothesis that should be an approximate best fit and function that generalizes the training data.
To understand this scheme, suppose we are in the case of a supervised learning (which is explained in point Types of Learning), in which for each data entry training, we know what will be its output. So; for the hypothesis in this type of learning, we need to get a function that fits the data training; or put another way, to minimize the “empirical Error ” error is measured after applying the hypothesis to the training data. Surely what matters is that the hypothesis obtained with the lowest possible error with the test data, but it is assumed that the training data are a sample representative enough so that the error with the test data is similar to the empirical errors.
In short, the goal of these techniques is to find that function or model (hypothesis); within the entire set of functions or models, that best fits the data and training generalizes to apply to test data and obtain a prediction, recommendation, classification etc.
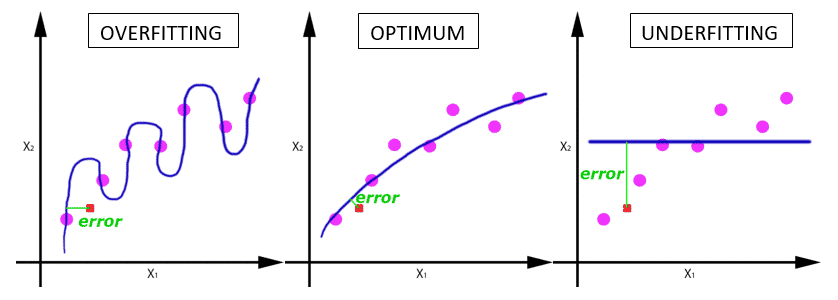
Overfitting and Underfitting
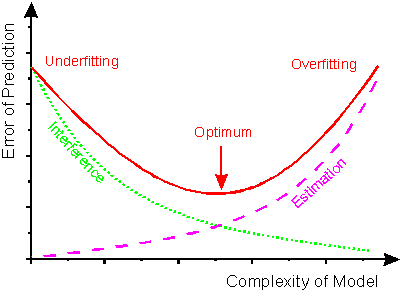
One of the most interesting points in the ML, it has been achieved learning by proper training data, obtaining a hypothesis able to correctly generalize the new input data. By contrast, getting a hypothesis as a result of overshooting (overfitting) or overgeneralization (Underfitting) of the training data, it will cause the output provided with new input data have (most likely) a very high error, which means say that the prediction will not be correct.
To see more detail the meaning of over fitting and under fitting, suppose the case of our expert system for predicting pools: We know that India national cricket team is one of the most powerful in the world and obviously in the Asia Cup league teams. By contrast there are more modest teams such as the Bangladesh that will fit in this case has lost more games than winning; but casually in the training data, we have three results that Bangladesh has won at India in their stadium. On the other hand in most of the training data we found that cricket matches played by India national cricket team settled with victory and another important fact is that 60% of the matches of the training data results in the victory of the home team.
With these data what would be the prediction of the outcome of the match “India Vs Bangladesh”?
Although this would be a summary of the data in the set of training data, a person (whether or not expert in cricket) and watching the training data could predict the outcome of this match would be a “1” (wins INDIA) because India national cricket team is one of the strongest teams, wins most matches, faces a team that lost more games than they win and also played in the stadium (60% of matches the local team wins). Although Machine learning algorithms have the ability to make these arguments (since these are made mathematically) if it is expected that the result is consistent and similar to what a human would. But, what result would throw the system if there is Overfitting or Underfitting?
- Overfitting(“India vs Bangladesh = Bangladesh Wins”): As in the set of training data has been so that there are only 3 clashes between these teams and Bangladesh is winning, according to the training data, so Bangladesh wins acc. To computer because it is the information that is available.
- Optimum(“India vs Bangladesh = India Wins“): Having overgeneralization the hypothesis yields results that will win the local team since 60% of the results are victories of local, therefore, in this the result would be correct.
- Underfitting(“India vs Bangladesh = Bangladesh Wins“): By analogy with the previous case, when the local team is Bangladesh, Bangladesh Wins.
What has been tried to explain in this long example is that the hypothesis obtained does not have to correctly predict 100% of cases, but if that should be required to some extent that generalizes correctly even if it means making specific errors. In other words, we must be able to find a hypothesis in which there is a balance between overfitting and overgeneralization.
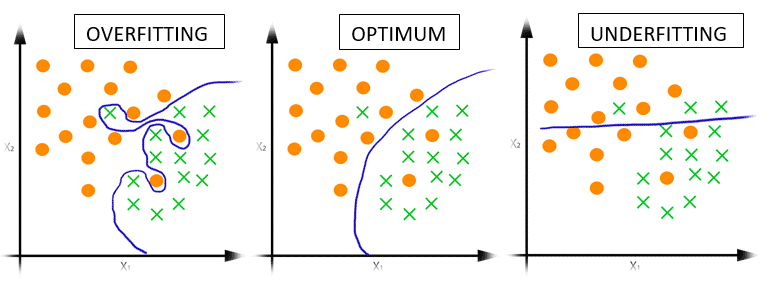
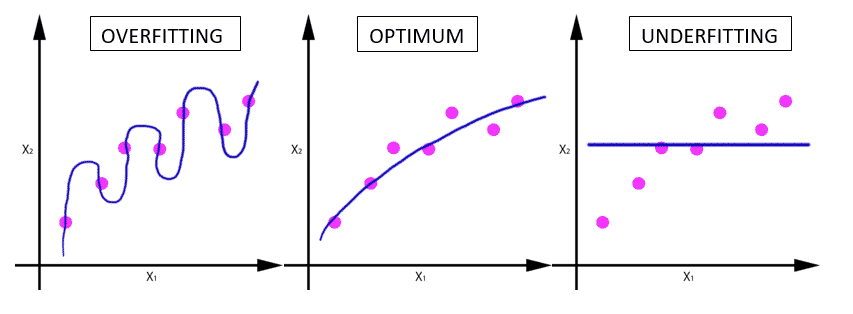
Now see graphically the concept of overfitting and Underfitting for classification and regression problems:
Getting a classifier that approximates f: R 2 → {*, x}:
Regression model that approximates f: R → R:
for example the case of regression, the error would be committed if we came a new input data (red dot), for each of the functions obtained:
Can be seen as the error with data test, it is higher in the case where overfitting and Underfitting occurs, and is less in the case in which widespread correctly, but obviously has a small error.
Learning types
Depending on the type of data that we have to train the system on, we can apply a type of learning or other. The following lists and explains the most common types of learning:
- Supervised learning: Type learning which has full information on the training data; i.e. the input data and the output thereof. It is the kind of learning that offers best result since it is the more information you have.
- Unsupervised Learning: Type of learning in which only available input data and aims to obtain information about the domain structure output.
- Semi-supervised learning: It is a type of hybrid learning between supervised and unsupervised learning.
- Adaptive Learning: Type of learning in which part of a previous model whose parameters are modified or adapted using the new training data.
- Learning online: In this type of learning there is no specific distinction between the test phase and training. The system learns (usually from zero) by the very process of prediction in which there is a human supervision is to validate or correct each output depending on the input.
- Reinforcement learning: Type of hybrid learning between online learning and semi-supervised learning in which supervision is incomplete; usually a type information {yes, no}, {0.1}, {reward, punishment}. It is a kind of learning that is based on the “argumentum ad baculum”, (Latin for “argument to the cudgel” or “appeal to the stick”) normally used in the train the animals.
Methods of evaluation of a system
To evaluate the hypothesis obtained after the application of some of the techniques of Machine Learning, you must have a data set (labeled or not) to generate the best possible empirical hypotheses and minimize error. Given a set of data, we can list the following evaluation methods depending on how the training data and test are divided:
- Validation: It is a very optimistic method in which all available data are used as test data and training.
- Partition (Hold Out): This method divides the data into two subsets: one training and one test. The problem with this method is that the test data for obtaining the hypothesis is wasted.
- Cross – validation (Cross Validation):This method divides the data randomly ‘N’ blocks. Each block is used as a test for a trained by the other system blocks. The drawback of this method is that it reduces the number of training data when the number of data of each block is large.
- Individual exclusion (Leaving one out):This method uses individual data as test data only a trained with all data except the system test. It is similar to cross – validation method, but in this case the computational cost is very large for the amount of phases of learning to be performed.
Machine Learning Techniques
It is truly complex to make a ranking or classification of ML techniques depending on the problems that can be solved. There are very specific techniques such as K-means or expectation-Maximization (EM) that are clearly used for problems Clustering and techniques however such as Support Vector Machine (SVM) or Neural Networks can fit regression both issues as classification, although they are more specific to the classification of regression. Whether each of the techniques can be classified in one way or another, so if it is obvious is that professionals ML should worry about properly learn the more technical best and thus have a high enough training as to learn to address and solve problems using the techniques that can adapt better.
Below is a classification of Machine Learning techniques and problems.
| Problems | Supervised learning | Clustering |
|
|
|
| Dimensionality reduction | Probabilistic models | Anomaly Detection |
|
|
|
| Neural Networks | Recommendation Systems | Theories |
|
|
|
Resources:
For further reading and learning on Machine Learning you can check open classroom at Stanford or grab this text book on Machine Learning by Tom M. Mitchell. CalTech Video Library and edX Online Course.