Are you ready to take your C++ programming skills to the next level? If you’re looking to enhance your understanding of data structures and algorithms, then you’ve come to the right place. In this comprehensive guide, we’ll dive deep into the world of min and max heaps in C++, equipping you with the knowledge and tools to master these fundamental data structures.
What exactly is a heap, you might wonder? Well, a heap is a specialized tree-based data structure that satisfies the heap property. It’s commonly used to efficiently store and retrieve the smallest or largest element, depending on whether it’s a min-heap or a max-heap. These powerful structures play a crucial role in various algorithms, making them essential for any programmer’s toolkit.
Throughout this guide, we’ll explore the characteristics, implementation, and use cases of both min and max heaps. We’ll provide clear examples and walk you through the process of implementing these data structures in the popular programming language, C++. By understanding their inner workings and nuances, you’ll gain a solid foundation for tackling complex problems and optimizing your code.
But that’s not all – we’ll go beyond the basics and compare the two heaps side by side. You’ll discover the key differences between min and max heaps, allowing you to choose the appropriate structure based on your specific needs. Whether you’re working on sorting algorithms, priority queues, or graph algorithms, knowing when to use a min or max heap can make a significant impact on your program’s efficiency.
So, if you’re ready to boost your data structure skills and elevate your programming abilities, join us on this exciting journey into the world of min and max heaps. Get ready to unravel their mysteries, harness their power, and unlock the true potential of your code. Let’s dive in!
What is Heap ?
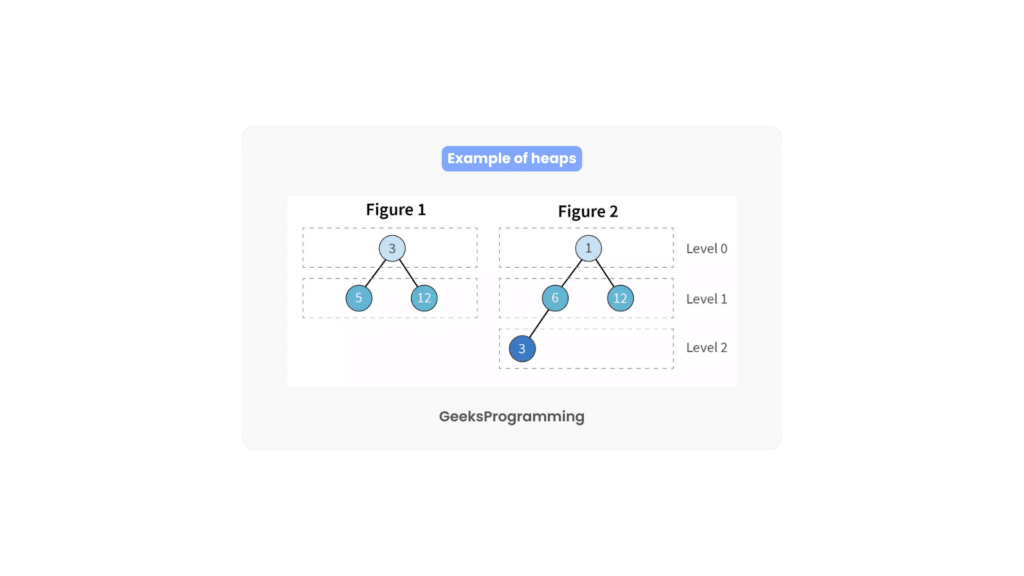
In simple terms, a heap is a specialized tree-based data structure that organizes elements in a particular order to facilitate efficient operations. One of its defining characteristics is that it forms a complete binary tree. Don’t worry if this sounds perplexing; we’ll break it down for you.
Imagine a tree structure where each node can have a maximum of two children. In a complete binary tree, all levels except the last one are completely filled, and the last level is filled from left to right. This arrangement ensures that the heap is compact and balanced, optimizing the performance of our operations.
But what truly sets a heap apart is its heap property. The heap property ensures that either the parent nodes are smaller than or equal to their children (min heap), or the parent nodes are larger than or equal to their children (max heap). This property is the secret sauce behind the heap’s efficiency.
Heaps excel at supporting two fundamental operations: insertion and deletion. When it comes to insertion, a heap makes it a breeze. You simply add the new element to the next available position in the complete binary tree and then adjust the tree to maintain the heap property. This process, known as “heapify”, guarantees the integrity of the heap while minimizing complexity.
Deletion is equally impressive. With a heap, removing the smallest or largest element (depending on whether it’s a min or max heap) is as easy as pie. Once the element is extracted, the heap is rearranged to restore the heap property swiftly and effortlessly.
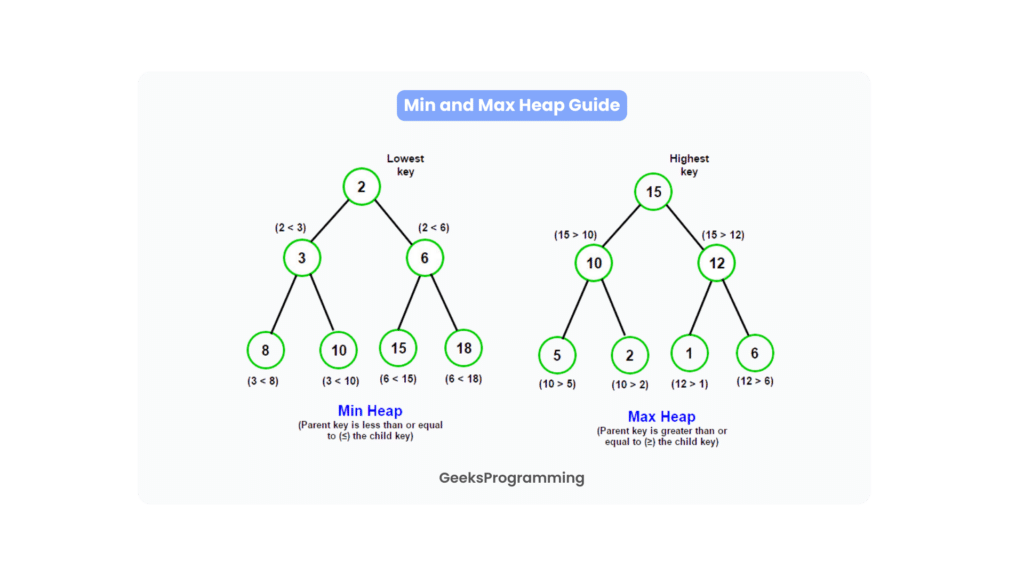
Min Heap and Max Heap
Let’s start by defining what a min heap is. Picture a complete binary tree where each parent node holds a value smaller than or equal to its children. The crucial aspect here is the “min” part, which indicates that the smallest element resides at the root of the tree. As you traverse down the levels, the values increase gradually. This arrangement empowers min heaps to facilitate efficient operations like extracting the minimum element swiftly, making them valuable in scenarios where you need to prioritize items based on their magnitude.
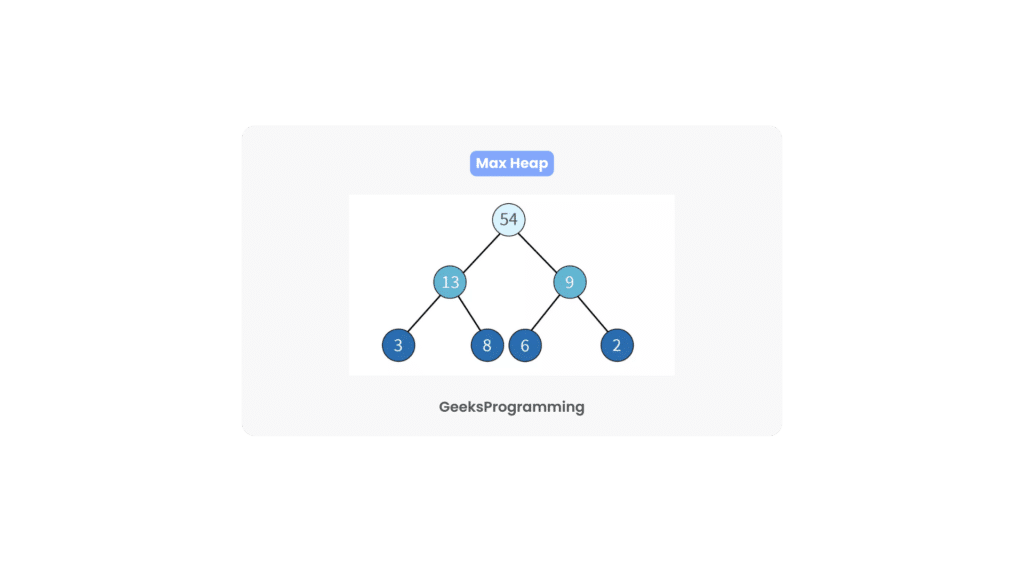
Now, let’s shift gears and explore max heaps. Similar to min heaps, max heaps are complete binary trees with an intriguing twist. In a max heap, the parent nodes always harbor values larger than or equal to their children. In essence, the “max” attribute ensures that the greatest element proudly claims its throne at the root. Descending through the levels reveals a gradual decrease in values, culminating in the leaves housing the smallest elements. Max heaps find utility in diverse applications, such as building priority queues that prioritize larger elements.
The secret behind maintaining the min or max property within a heap lies in the process known as “heapify”. Heapify is a crucial operation that ensures the correct ordering of elements in the heap.
In a min heap, when a new element is inserted or a value is modified, “heapify” compares the element with its parent node. If the news element is smaller than its parent, they swap positions, allowing the smaller value to rise towards the root. This process continues recursively until the min heap property is restored throughout the entire tree. As a result, the smallest element always resides at the top, while the remaining elements cascade downwards in ascending order.
Conversely, in a max heap, “heapify” operates in a similar fashion but with a different objective. When a new element is added or a value is modified, it compares the element with its parent. If the new element is larger than its parent, they exchange places, enabling the larger value to ascend towards the root. This recursive process persists until the max heap property reigns supreme across the entire structure. Consequently, the largest element remains firmly positioned at the top, while the rest of the elements descend in descending order.
By performing “heapify” operations whenever necessary, both min heaps and max heaps maintain their respective characteristics and ensure that the parent-child relationships within the heap always align with the desired property.
Whether you’re dealing with a min heap or a max heap, these data structures boast remarkable properties. Both heaps guarantee that the tree remains balanced, ensuring efficient insertion and deletion operations. Furthermore, heaps can be easily implemented using arrays, which enhances their practicality in programming.
Algorithms Utilizing Heap Data Structures
When it comes to efficient data manipulation and retrieval, heap data structures are an invaluable tool in the arsenal of any programmer. By understanding how to leverage the power of heaps, we can optimize various algorithms and tackle complex problems with ease. In this section, we will explore some key algorithms that heavily rely on heap data structures: heap sort and priority queues.
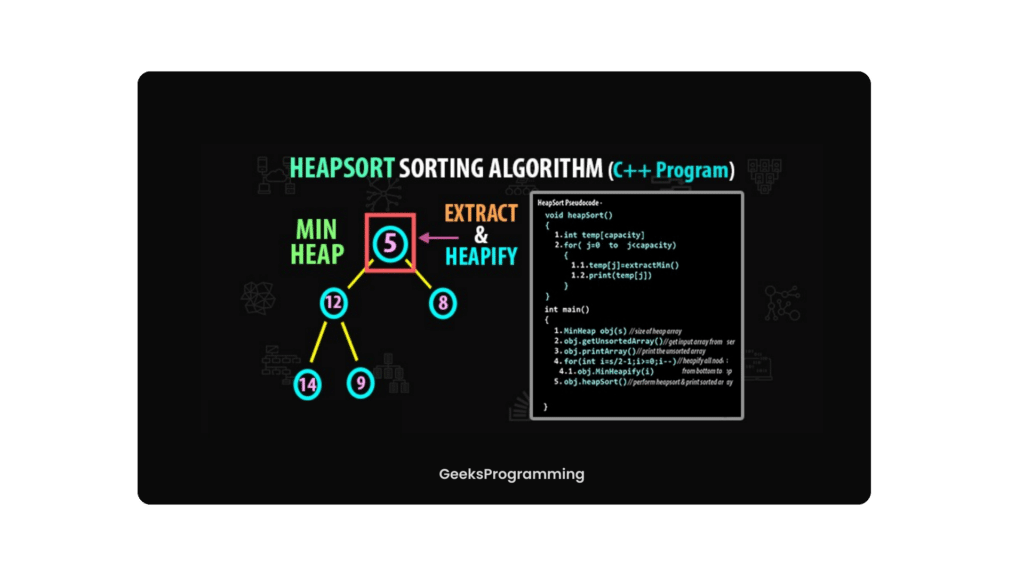
Heap sort is a sorting algorithm that utilizes the inherent properties of heaps to efficiently arrange elements in ascending or descending order. By building a max heap (or a min heap, depending on the desired sorting order), heap sort maintains the heap property, which guarantees that the parent node is either greater (or smaller) than its children. This property allows us to effortlessly extract the maximum (or minimum) element from the heap and place it at the appropriate position in the sorted array. The remaining elements are then “heapified”, and the process is repeated until the entire array is sorted. With its time complexity of O(n log n) and in-place sorting nature, heap sort stands as a powerful algorithm for large datasets.
Another algorithm that relies on heap data structures is the priority queue. A priority queue is an abstract data type that enables efficient retrieval of the most prioritized element. It serves as a versatile tool in various applications, such as job scheduling, event handling, and graph algorithms. Under the hood, priority queues utilize heaps to maintain the order of elements based on their priority. By employing a max heap for a maximum priority queue (or a min heap for a minimum priority queue), the most significant element can be accessed in constant time, resulting in an efficient retrieval process.
Understanding the functionality of priority queues and their utilization of heap data structures is crucial for optimizing algorithms that require efficient element prioritization. By combining the power of heaps and priority queues, we can solve complex problems, such as finding the shortest path in a graph or efficiently processing tasks with varying priorities.
Implementation of Min and Max Heap in C++ With Examples
Let’s dive right into the exciting part – coding! It’s time to fire up our C++ compilers and witness the power of heaps in action. Get ready to roll up your sleeves and delve into the practical implementation of min and max heaps.
To begin, let’s create a new C++ file and include the necessary headers:
#include <iostream>
#include <vector>
#include <algorithm>
Next, we’ll define our main function and start implementing a min heap. For the sake of simplicity, let’s work with integers.
int main() {
std::vector<int> minHeap;
// Inserting elements into the min heap
minHeap.push_back(9);
minHeap.push_back(4);
minHeap.push_back(7);
minHeap.push_back(2);
minHeap.push_back(1);
// Building the min heap property
std::make_heap(minHeap.begin(), minHeap.end(), std::greater<int>());
// Accessing the minimum element (root)
int minElement = minHeap.front();
std::cout << "Minimum element: " << minElement << std::endl;
// Deleting the minimum element
std::pop_heap(minHeap.begin(), minHeap.end(), std::greater<int>());
minHeap.pop_back();
// Accessing the new minimum element (after deletion)
minElement = minHeap.front();
std::cout << "New minimum element: " << minElement << std::endl;
return 0;
}
```
//Now, let's move on to implementing a max heap:
```(C++)
int main() {
std::vector<int> maxHeap;
// Inserting elements into max heap
maxHeap.push_back(9);
maxHeap.push_back(4);
maxHeap.push_back(7);
maxHeap.push_back(2);
maxHeap.push_back(1);
// Building the max heap property
std::make_heap(maxHeap.begin(), maxHeap.end());
// Accessing the maximum element (root)
int maxElement = maxHeap.front();
std::cout << "Maximum element: " << maxElement << std::endl;
// Deleting the maximum element
std::pop_heap(maxHeap.begin(), maxHeap.end());
maxHeap.pop_back();
// Accessing the new maximum element (after deletion)
maxElement = maxHeap.front();
std::cout << "New maximum element: " << maxElement << std::endl;
return 0;
}
Now, compile and run your code, and witness the magic of heaps firsthand! You should see the minimum and maximum elements being displayed, along with the updated values after deletion.
It’s important to note that in the previous scenario, we completed the vector by adding all the elements and then converted it into a heap. However, there’s an alternative approach where we make it a heap from the beginning and perform “heapify” operations when adding elements. This approach allows us to modify the array even after making it a heap, without compromising the heap property of the vector.
Instead of adding elements first and then using push_heap to maintain the heap property, we can directly make the vector a heap and perform “heapify” operations during the addition of elements. This approach offers more flexibility when working with the array.
Here’s how we can modify the previous code to follow this alternative approach for both max and min heaps:
int main() {
std::vector<int> maxHeap;
std::vector<int> minHeap;
// Make the vectors heaps without any elements initially
std::make_heap(maxHeap.begin(), maxHeap.end());
std::make_heap(minHeap.begin(), minHeap.end(), std::greater<int>());
// Insert elements into the heaps
maxHeap.push_back(9);
std::push_heap(maxHeap.begin(), maxHeap.end());
minHeap.push_back(9);
std::push_heap(minHeap.begin(), minHeap.end(), std::greater<int>());
// Access the maximum and minimum elements
int maxElement = maxHeap.front();
int minElement = minHeap.front();
// Delete the maximum and minimum elements
std::pop_heap(maxHeap.begin(), maxHeap.end());
maxHeap.pop_back();
std::pop_heap(minHeap.begin(), minHeap.end(), std::greater<int>());
minHeap.pop_back();
return 0;
}
By following this modified approach, we can add or remove elements from the heap vector even after it has been made a heap, allowing for more flexibility in managing the data.
By getting hands-on experience with these code examples, you’ll solidify your understanding of heaps in C++ and pave the way for exploring more complex applications. So, embrace the power of coding and let the heaps unfold their full potential in your programs!
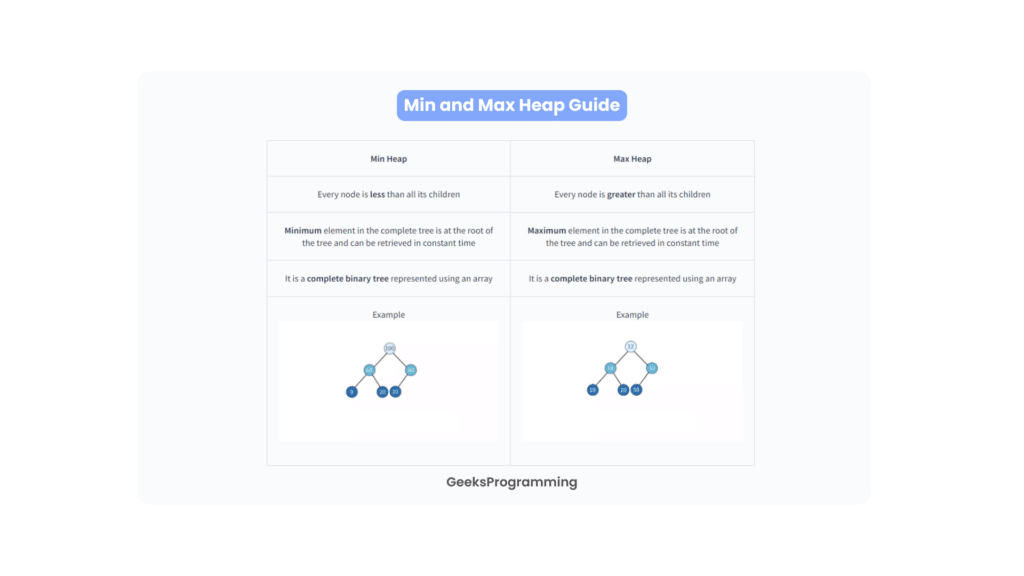
Difference Between Min Heap and Max Heap in C++
Let’s start with the basics. Both min heaps and max heaps are binary trees that satisfy the heap property, which ensures that the value of each node is either greater or smaller than its child nodes. However, the key distinction lies in how this property is applied.
A min heap guarantees that the parent node has a smaller value than its children. This means that the smallest element is always at the root of the heap. On the other hand, a max heap ensures that the parent node has a greater value than its children, placing the largest element at the root.
So, when should you use a min heap versus a max heap? Well, it depends on the problem you’re trying to solve. If you’re working on tasks that involve finding the smallest element, such as priority queues or implementing Dijkstra’s algorithm for finding the shortest path, a min heap is your best bet. It allows you to quickly extract the minimum element in logarithmic time, making it highly efficient for such use cases.
Conversely, if you’re dealing with scenarios where you need to find the largest element, such as implementing a heap sort or priority queues that prioritize the largest elements, a max heap is the way to go. With a max heap, the largest element is readily available at the root, making it efficient for retrieval.
Conclusion
In conclusion, mastering min and max heaps is an essential step in elevating your data structure skills and optimizing your programming abilities. These powerful tree-based data structures play a vital role in various algorithms, enabling efficient storage, retrieval, and prioritization of elements. By understanding the characteristics, implementation, and use cases of min and max heaps, you’ll gain a solid foundation for tackling complex problems and optimizing your code.
Min heaps excel at extracting the minimum element swiftly, making them ideal for scenarios where prioritizing items based on their magnitude is crucial. On the other hand, max heaps prioritize larger elements and find utility in diverse applications like building priority queues.
The “heapify” operation lies at the heart of maintaining the min or max property within a heap. By recursively comparing and swapping elements as necessary, the integrity of the heap is preserved, ensuring efficient insertion, deletion, and manipulation operations.
Heap data structures also serve as the backbone for important algorithms like heap sort and priority queues. Heap sort leverages the properties of heaps to efficiently arrange elements in ascending or descending order, while priority queues utilize heaps to retrieve the most prioritized element efficiently.
To put theory into practice, we explored the implementation of min and max heaps in C++. By using the std::make_heap, std::pop_heap, and other functions from the <algorithm> library, we can create and manipulate heaps seamlessly.
So, don’t hesitate to embark on this exciting journey into the world of min and max heaps. Unravel their mysteries, harness their power, and unlock the true potential of your code. By mastering these fundamental data structures, you’ll empower yourself to tackle complex programming challenges with confidence. Happy coding!


