The pascal’s triangle Algorithm is the most popular algorithm that every beginner or a student come across at least once. The algorithm will be very much similar to the one printing pyramid shapes in console screen. The pascal’s triangle algorithm output will be also looking very similar but instead of printing all 1s or 0s, we should be printing numbers in a special order that makes it very unique.
The number of elements for each row will be same as the row number (i.e first row contains one element and the second row contains two elements, etc). The first row starts with the value “1”. The first and last elements of the each row will be the value “1”. The rest of the values will be summation of the two adjacent elements of the previous row. Assume that we are going to fill the third row. The first and last value is always the value “1”. The second element value would be summation of the previous row adjacent elements (i.e) “1” and “1”, so the result is “2”.
The sample output can be seen below.
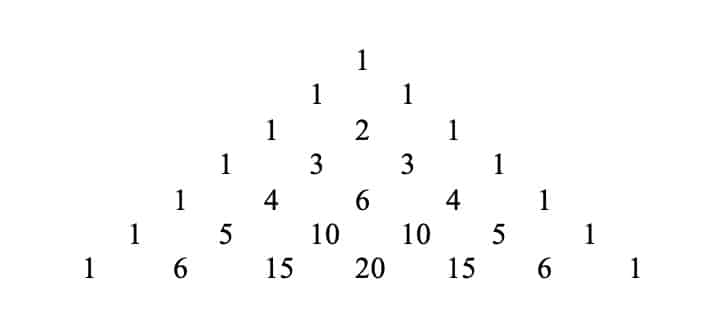
There are two main challenges to implement the algorithm. The first challenge is to print the numbers in the required pattern. The pattern requires elements to be print in a full pyramid shape with sufficient spaces between each elements. The second challenge would be computing the value to be filled in to the full pyramid.
We are going to implement the algorithm step by step, which each step we will attain certain state of the program. We are going to implement the same algorithm using two of the very famous programming language C++ and Java. Most of the syntax will be common among these languages.
For the Java language, we need to download and install the latest version of the JDK from the following link which provides the development environment to develop the Java code. https://www.oracle.com/java/technologies/downloads/
For the C++ language, we can use DevC++ or Visual Studio IDE. The latest version of the DevC++ tool can be downloaded from the following link. https://sourceforge.net/projects/orwelldevcpp/
Pascal's Triangle Implementation - First Challenge
STEP #1
The step one would be declaring and initializing all the required libraries that we need to run and invoke the basic programming API. The basic API includes printing the characters into the console screen.
Whoever follows the C++ language, create a new file with the extension of *.cpp and copy – paste the code below. The code can be compiled and executed using the DevC++ tool.
C++
#include <iostream>
using namespace std;
int main()
{
}
Whoever follows the Java language, create a file called “Main.java” and copy – paste the code below. The code can be compiled and executed using the commands
>javac Main.java [To compile]
>java Main [To execute]
JAVA
public class Main
{
public static void main(String[] args) {
}
}
The output of the step one will be an empty screen with no compilation errors or warnings.
STEP #2
The step two is to extend the same code with a main for loop that should iterate N times, where N is the height of the Pascal’s triangle. We are going to assume that the value of N is always 5. Declare an integer variable named N with the value 5. The for loop counter variable name will be “i” and the exit condition of the loop should be “i < N”.
C++
#include <iostream>
using namespace std;
int main()
{
int N = 5;
for(int i = 0; i < N; i++)
{
}
}
The syntax of declaring an integer variable for N count and implementing for loop in the Java language will be exactly same as the language C++.
Java
public class Main
{
public static void main(String[] args) {
int N = 5;
for(int i = 0; i < N; i++)
{
}
}
Step #3
The next step is to create an inner for loop to print the initial neccesary spaces before printing the numbers. The loop should iterate (N – i) times, where “i” is the first loop counter. The initial spaces should start printing N number of tabs decreasing to per each iteration.
The exit condition of the inner for loop would be “j < N – i”
The C++ language uses cout statement to print anything into the console output.
C++
#include <iostream>
using namespace std;
int main()
{
int N = 5;
for(int i = 0; i < N; i++)
{
for(int j = 0; j < N - i; j++)
{
cout << "\t";
}
}
}
The Java language uses System.out.print() statement to print anything into the console output.
Java
public class Main
{
public static void main(String[] args) {
int N = 5;
for(int i = 0; i < N; i++)
{
for(int j = 0; j < N - i; j++)
{
System.out.print("\t");
}
}
}
Step #4
Lets start printing some character in order to test the algorithm such that it should print sufficient tabs along with the character.
C++
#include <iostream>
using namespace std;
int main()
{
int N = 5;
for(int i = 0; i < N; i++)
{
for(int j = 0; j < N - i; j++)
{
cout << "\t";
}
cout << "X";
cout << endl;
}
}
JAVA
public class Main
{
public static void main(String[] args) {
int N = 5;
for(int i = 0; i < N; i++)
{
for(int j = 0; j < N - i; j++)
{
System.out.print("\t");
}
System.out.print("X");
System.out.println();
}
}
The output of the step would be something like this,
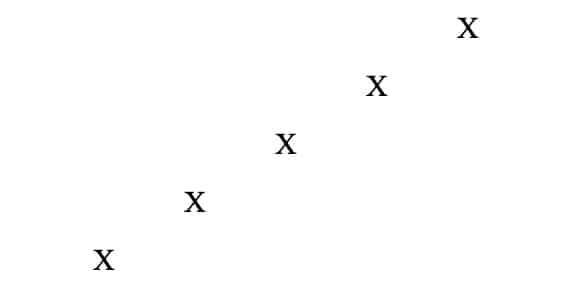
Step #5
The next step is to duplicate the same decided character “X” as many times as the row number. In our case, the row number is (i + 1) as the for loop counter we use starts with 0, we should increment by one in order to start with 1.
C++
#include <iostream>
using namespace std;
int main()
{
int N = 5;
for(int i = 0; i < N; i++)
{
for(int j = 0; j < N - i; j++)
{
cout << "\t";
}
for(int j = 0; j < (i + 1); j++)
{
cout << "X" << "\t\t";
}
cout << endl << endl;
}
}
Java
public class Main
{
public static void main(String[] args) {
int N = 5;
for(int i = 0; i < N; i++)
{
for(int j = 0; j < N - i; j++)
{
System.out.print("\t");
}
for(int j = 0; j < (i + 1); j++)
{
System.out.print("X");
System.out.print("\t\t");
}
System.out.println();
System.out.println();
}
}
}
We used to print two “tab” character as we need to fill the adjacent elements of the next row elements not in the same column. For eg, the value “1” of the first row will not be in the same column as the second row value “1”.
We also print two new lines after the inner for loop as it will make the pyramid looks even better.
The output of the following code will be as below,
The first challenge of the algorithm is done. We have obtained the perfect shape of the full pyramid.
Second Challenge in Implementation of Pascals Triangle
Step #1
The second challenge of the algorithm is to compute which value to be print in each row and column. As the first step of the algorithm, lets replace the character “X” with an integer value. Lets declare an integer value called “value” and assign value “1”. Instead of printing the character “X”, print the integer value.
#include <iostream>
using namespace std;
int main()
{
int N = 5;
for(int i = 0; i < N; i++)
{
for(int j = 0; j < N - i; j++)
{
cout << "\t";
}
int value = 1;
for(int j = 0; j < (i + 1); j++)
{
cout << value << "\t\t";
}
cout << endl << endl;
}
}
Java
public class Main
{
public static void main(String[] args) {
int N = 5;
for(int i = 0; i < N; i++)
{
for(int j = 0; j < N - i; j++)
{
System.out.print("\t");
}
int value = 1;
for(int j = 0; j < (i + 1); j++)
{
System.out.print(value);
System.out.print("\t\t");
}
System.out.println();
System.out.println();
}
}
}
Step #2
Before we get into the actual computation of the value, we should have some idea about permutation and combinations. The permutation is a way to get to know the number of possibilities that a subset of elements can be rearranged without replacing one with other.
nPr = n! / (n – r)!
where the n represents number of total elements to be permuted and r represents number of sub-set that we should permutate. The symbol “!” represents factorial of that number (i.e n x (n-1) x …. x 2 x 1).
Similarly, Combination is the number of possibilities that a set of elements can be combined into a sub-set with replacement allowed.
nCr = n! / r! (n – r)!
We are going to introduce a new method to compute the factorial of an integer number. The method should take an argument and call the method itself recursively with one number less than the argument until the number becomes less than or equal to 1.
C++
#include <iostream>
using namespace std;
int factorial(int n)
{
if(n <= 1)
return 1;
return n * factorial(n – 1);
}
Java
public class Main
{
public static int factorial(int n) {
if(n <= 1)
return 1;
return n * factorial(n – 1);
}
}
Step #3
The final step of the algorithm is to use the method written in the step #2 and compute the combination formula with n as the first loop counter variable and r as the inner loop counter variable.
C++
#include <iostream>
using namespace std;
int factorial(int n)
{
if(n <= 1)
return 1;
return n * factorial(n – 1);
}
int main()
{
int N = 5;
for(int i = 0; i < N; i++)
{
for(int j = 0; j < N - i; j++)
{
cout << "\t";
}
int value = 1;
for(int j = 0; j < (i + 1); j++)
{
value = factorial(i) / (factorial(j) * factorial(i - j));
cout << value << "\t\t";
}
cout << endl << endl;
}
}
Java
public class Main
{
public static int factorial(int n) {
if(n <= 1)
return 1;
return n * factorial(n – 1);
}
public static void main(String[] args) {
int N = 5;
for(int i = 0; i < N; i++)
{
for(int j = 0; j < N - i; j++)
{
System.out.print("\t");
}
int value = 1;
for(int j = 0; j < (i + 1); j++)
{
value = factorial(i) / (factorial(j) * factorial(i - j));
System.out.print(value);
System.out.print("\t\t");
}
System.out.println();
System.out.println();
}
}
}
The output of the final version of the algorithm will be as below.

We will get a pascal’s triangle of height 5 as we have hard coded the value N as 5. We can extend the code by getting the value of N as input from user or we can change the value N from 5 to any desired number.
The algorithm`s output with the N value provided as “8” will be as below.
Time complexity
The time complexity of the Pascal’s Triangle algorithm would be measure by computing the number of times a core statement of the code is been executing. The algorithm`s core statement would be calculating the value to be printed for each row and column of the triangle and the print statement itself.
These core statements are written inside the inner for loop which is already inside the outer main for loop. The number of times outer main for loop executes is N times. The inner for loop is based on the outer for loop counter times (i.e i times). At most the inner for loop will be executed N times. Hence the time complexity of the pascal’s triangle is
Time Complexity = O(N2)
So that’s all about implementing Pascal’s Triangle in C++ and Java. If you still struggle to understand the intricacies of Pascal’s Triangle or any other Algorithm and need help with C++ programming or Java Programming Help, then reach out to us and get an expert tutor to help with your programming difficulties.





