Depth First Search Algorithm
The Depth First Search algorithm is a traversal algorithm used to either search or iterate elements from a tree or from a graph. The search algorithm gives priority to iterating elements deeper rather than breadth-wise. The algorithm will not visit a node that is already visited.
Sample of DFS with Diagram
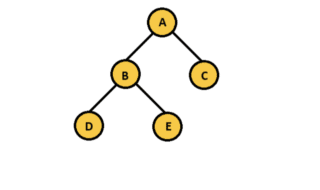
Assume the tree below,
The DFS algorithm starts iteration by visiting node “A” first and visits its one of its child node second (the first child node would be node “B”). The third visit rather than visiting the second child node “C”, the algorithm goes deeper into the child node of the node “B” ( the first child node of node “B” is node “D”). There is no child node for the node “D”, hence the iteration goes back to node “B” which is already visited. The algorithm takes the next child of Node “B” which is node “E”. After visiting node “E”, backtrack to node “B”. The node “B” doe not have any more child nodes to iterate, hence the algorithm backtrack again to node “A”. The algorithm repeats the same action recursively until all the nodes are visited.
DFS Path :
A => B => D => E => C
The other alternative searching algorithm is called BFS ( Breadth First Search) algorithm. The BFS algorithm is used to iterate all the child nodes of the current node first rather than going deeper.
BFS Path :
A => B => C => D => E
We uses graph instead of tree which would be very much interesting while implementing the algorithm. We are going to implement the algorithm step by step, which each step we will attain certain state of the program. We are going to implement the same algorithm using two of the very famous programming language Java and Python. Most of the syntax will be common among these languages. For the Java language, we need to download and install the latest version of the JDK from the following link which provides the development environment to develop the Java code.
https://www.oracle.com/java/technologies/downloads/
For the Python language, we can use any IDE along with the python development toolkit. The latest version of the toolkit can be downloaded from the following link.
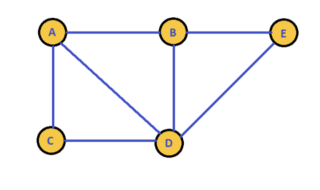
Graph of Traversal Algorithms
Lets have a brief walk through about the data structure “Graph” before we start implementing the DFS algorithm. A graph is a non-linear data structure, which is similar to the tree data structure. The graph has several nodes which will not have any levels of connectivity like trees instead the nodes can have connectivity to any number of nodes and any levels.
The above graph has five nodes with each node has several connections. The node “A” connects with three nodes “B”, “C” and “D”. The node “B” has connections with three nodes “A”, “D” and “E”. The above graph is an un-directional graph which does not have any directions defined, similarly there is another type of graph called a directional graph which has directional arrows representing which node path goes to which node. Let’s implement the graph data structure before we implement the DFS algorithm.
Implementation Graph Data Structure
Step #1
Step one would be declaring and initializing all the required libraries that we need to run and invoke the basic programming API. The basic API includes printing the characters into the console screen and create an empty class. Whoever follows the python language, create a new file with the extension of *.py and copy-paste the code below. The code can be compiled and executed using the following command.
python3 Graph.py
Python
class Graph:
def __init__(self):
print ('init')
Whoever follows the Java language, create a file called “Main.java” and copy – paste the code below. The code can be compiled and executed using the commands
javac Graph.java [To compile]
>java Graph [To execute]
Java
public class Graph
{
public static void main(String[] args) {
}
}
The output of step one will be an empty screen with no compilation errors or warnings.
Step #2
Step two is to declare the required data members to hold the nodes and edges of the graph. We are going to use an integer variable to hold the number of edges and an array of an array to hold the edges of each node.
Python
class Graph:
N = 0
nodes = []
def __init__(self):
print ('init')
Java
import java.io.*;
import java.util.*;
public class Graph
{
private int N;
private ArrayList<ArrayList<Integer>> nodes;
public static void main(String[] args) {
}
}
Step #3
The next step is to initialize the data members that we have declared in the previous step. We will be creating N number of empty arrays in order to hold the edges of each node. Declare a for loop to initialize N number of arrays of holding edges.
Python
class Graph:
N = 0
nodes = []
def __init__(self):
self.N = N
self.nodes = []
for u in range(N):
self.nodes.append([])
Java
import java.io.*;
import java.util.*;
public class Graph
{
private int N;
private ArrayList<ArrayList<Integer>> nodes;
public Graph(int n)
{
this.N = n;
this.nodes = new ArrayList<ArrayList<Integer>>();
for (int i = 0; i < this.N; ++i)
this.nodes.add(new ArrayList<Integer>());
}
public static void main(String[] args) {
}
}
Step 4
Lets create a new method which provides a functionality to add edges for a node. The function takes two parameters u and v. The parameter, u represents the node into which we are going to add the edge. The parameter v represents the node to which the edge going to connect. The method will add the parameter v into the edge array at the index of u.
Python
class Graph:
N = 0
nodes = []
def __init__(self):
self.N = N
self.nodes = []
for u in range(N):
self.nodes.append([])
def addEdge(self, u, v):
self.nodes[u].append(v)
Java
import java.io.*;
import java.util.*;
public class Graph
{
private int N;
private ArrayList<ArrayList<Integer>> nodes;
public Graph(int n)
{
this.N = n;
this.nodes = new ArrayList<ArrayList<Integer>>();
for (int i = 0; i < this.N; ++i)
this.nodes.add(new ArrayList<Integer>());
}
public void addEdge(int u, int v)
{
this.nodes.get(u).add(v);
}
public static void main(String[] args) {
}
}
Step 5
class Graph:
N = 0
nodes = []
def __init__(self):
self.N = N
self.nodes = []
for u in range(N):
self.nodes.append([])
def addEdge(self, u, v):
self.nodes[u].append(v)
graph = Graph(5)
graph.addEdge(0, 1) # A => B
graph.addEdge(0, 2) # A => C
graph.addEdge(0, 3) # A => D
graph.addEdge(1, 0) # B => A
graph.addEdge(1, 3) # B => D
graph.addEdge(1, 4) # B => E
graph.addEdge(2, 0) # C => A
graph.addEdge(2, 3) # C => D
graph.addEdge(3, 0) # D => A
graph.addEdge(3, 1) # D => B
graph.addEdge(3, 2) # D => C
graph.addEdge(3, 4) # D => E
graph.addEdge(4, 1) # E => B
graph.addEdge(4, 3) # E => D
Java
import java.io.*;
import java.util.*;
public class Graph
{
private int N;
private ArrayList<ArrayList<Integer>> nodes;
public Graph(int n)
{
this.N = n;
this.nodes = new ArrayList<ArrayList<Integer>>();
for (int i = 0; i < this.N; ++i)
this.nodes.add(new ArrayList<Integer>());
}
public void addEdge(int u, int v)
{
this.nodes.get(u).add(v);
}
public static void main(String[] args) {
Graph graph = new Graph(5);
graph.addEdge(0, 1); // A => B
graph.addEdge(0, 2); // A => C
graph.addEdge(0, 3); // A => D
graph.addEdge(1, 0); // B => A
graph.addEdge(1, 3); // B => D
graph.addEdge(1, 4); // B => E
graph.addEdge(2, 0); // C => A
graph.addEdge(2, 3); // C => D
graph.addEdge(3, 0); // D => A
graph.addEdge(3, 1); // D => B
graph.addEdge(3, 2); // D => C
graph.addEdge(3, 4); // D => E
graph.addEdge(4, 1); // E => B
graph.addEdge(4, 3); // E => D
}
}
Implementation BFS Algorithm
Step 1
We are going to implement a method to perform DFS search by extending the Graph class written. The method prints the visited nodes and marks the node as visited. We will be using a boolean array in order to hold the state of whether a node is visited or not. Let’s add an array as a data member of the class.
Python
Java
import java.io.*;
import java.util.*;
public class Graph
{
private int N;
private ArrayList<ArrayList<Integer>> nodes;
private ArrayList<Boolean> visited;
public Graph(int n)
{
this.N = n;
this.nodes = new ArrayList<ArrayList<Integer>>();
this.visited = new ArrayList<Boolean>();
for (int i = 0; i < this.N; ++i)
{
this.nodes.add(new ArrayList<Integer>());
this.visited.add(false);
}
}
public void addEdge(int u, int v)
{
this.nodes.get(u).add(v);
}
public static void main(String[] args) {
Graph graph = new Graph(5);
graph.addEdge(0, 1); // A => B
graph.addEdge(0, 2); // A => C
graph.addEdge(0, 3); // A => D
graph.addEdge(1, 0); // B => A
graph.addEdge(1, 3); // B => D
graph.addEdge(1, 4); // B => E
graph.addEdge(2, 0); // C => A
graph.addEdge(2, 3); // C => D
graph.addEdge(3, 0); // D => A
graph.addEdge(3, 1); // D => B
graph.addEdge(3, 2); // D => C
graph.addEdge(3, 4); // D => E
graph.addEdge(4, 1); // E => B
graph.addEdge(4, 3); // E => D
}
}
Step 2
The next step is to implement the method. The method takes one parameter whose default value is “0” (i.e) the iteration starts from the 0 th node. The method checks if the node is already visited, if then the method just returns. If not, print the node number in to output console and mark the node visited by assigning the specific index of the visited array as True. The method then iterates through all the edge nodes of the current node and call the same DFS method recursively.
Python
class Graph:
N = 0
nodes = []
visited = []
def __init__(self):
self.N = N
self.nodes = []
self.visited = []
for u in range(N):
self.nodes.append([])
self.visited.append(False)
def addEdge(self, u, v):
self.nodes[u].append(v)
def DFS(self, u = 0):
if(self.visited[u] == True):
return
print(u)
self.visited[u] = True
for v in self.nodes[u]:
self.DFS(v)
graph = Graph(5)
graph.addEdge(0, 1) # A => B
graph.addEdge(0, 2) # A => C
graph.addEdge(0, 3) # A => D
graph.addEdge(1, 0) # B => A
graph.addEdge(1, 3) # B => D
graph.addEdge(1, 4) # B => E
graph.addEdge(2, 0) # C => A
graph.addEdge(2, 3) # C => D
graph.addEdge(3, 0) # D => A
graph.addEdge(3, 1) # D => B
graph.addEdge(3, 2) # D => C
graph.addEdge(3, 4) # D => E
graph.addEdge(4, 1) # E => B
graph.addEdge(4, 3) # E => D
graph.DFS()
Java
Instead of using the default valued parameter in java, we use another overload of the the same method with no parameters and the method will simply redirect the call to another the method with the value “0” as starting node.
import java.io.*;
import java.util.*;
public class Graph
{
private int N;
private ArrayList<ArrayList<Integer>> nodes;
private ArrayList<Boolean> visited;
public Graph(int n)
{
this.N = n;
this.nodes = new ArrayList<ArrayList<Integer>>();
this.visited = new ArrayList<Boolean>();
for (int i = 0; i < this.N; ++i)
{
this.nodes.add(new ArrayList<Integer>());
this.visited.add(false);
}
}
public void addEdge(int u, int v)
{
this.nodes.get(u).add(v);
}
public void DFS(int u)
{
if(visited.get(u) == true)
return;
visited.set(u, true);
System.out.println(u);
for (int i = 0; i < this.nodes.get(u).size(); ++i)
{
DFS(this.nodes.get(u).get(i));
}
}
public void DFS()
{
DFS(0);
}
public static void main(String[] args) {
Graph graph = new Graph(5);
graph.addEdge(0, 1); // A => B
graph.addEdge(0, 2); // A => C
graph.addEdge(0, 3); // A => D
graph.addEdge(1, 0); // B => A
graph.addEdge(1, 3); // B => D
graph.addEdge(1, 4); // B => E
graph.addEdge(2, 0); // C => A
graph.addEdge(2, 3); // C => D
graph.addEdge(3, 0); // D => A
graph.addEdge(3, 1); // D => B
graph.addEdge(3, 2); // D => C
graph.addEdge(3, 4); // D => E
graph.addEdge(4, 1); // E => B
graph.addEdge(4, 3); // E => D
graph.DFS();
}
}
Final Output
0
1
3
2
4
Time Complexity
The time complexity of the algorithm would be measure by computing the number of times a core statement of the code is been executing. The algorithm’s core statement would be iterating each node and marking it as “visited”. The method call will happen exactly once per node as we are not allowing the method to execute if the node is already visited. Hence the time taken is the same as the N (number of nodes).
Time Complexity = O(N)
Breadth First Search
The implementation of the BFS algorithm will be very much similar to the DFS algorithm. The only difference is instead of going deeper into all the children’s nodes recursively, visiting the sibling nodes first. Assume the below graph,
The BFS path would be,
A => B => C => D => E
The algorithm will visit all the children nodes of the starting node “A”, which are “B”, “C” and “D”. After visiting all the children nodes, now going deeper to the sub-nodes of all the children nodes. The only un-visited node remaining would be the node “E”.
Implementation of Breath First Search step by step
Step 1
The implementation involves a queue data structure instead of calling the method recursively. The method will first print the element and add the starting element into the queue and make its visited state True.
Python
def BFS(self):
u = 0
queue = []
self.visited[u] = True
queue.append(u)
print(u)
Java
public class Graph
{
public void BFS()
{
int u = 0;
Queue<Integer> queue = new LinkedList<>();
System.out.println(u);
visited.set(u, true);
queue.add(u);
}
}
Step 2
The next step is to create a loop that should iterate until the queue is empty. For each iteration, the head value of the queue is popped and used as the current node.
Python
def BFS(self):
u = 0
queue = []
self.visited[u] = True
queue.append(u)
print(u)
while len(queue) > 0:
u = queue.pop(0)
Java
public class Graph
{
public void BFS()
{
int u = 0;
Queue<Integer> queue = new LinkedList<>();
System.out.println(u);
visited.set(u, true);
queue.add(u);
while (queue.size() != 0)
{
u = queue.peek();
queue.remove();
}
}
}
Step 3
The edge nodes of the current node will be then iterated and check if the node is not visited. If then print the current edge node v and set the visited boolean as True. The edge node v is then printed and added to the queue.
Python
def BFS(self):
u = 0
queue = []
self.visited[u] = True
queue.append(u)
print(u)
while len(queue) > 0:
u = queue.pop(0)
for v in self.nodes[u]:
if(self.visited[v] == False):
self.visited[v] = True
queue.append(v)
print(v)
Java
public class Graph
{
public void BFS()
{
int u = 0;
Queue<Integer> queue = new LinkedList<>();
System.out.println(u);
visited.set(u, true);
queue.add(u);
while (queue.size() != 0)
{
u = queue.peek();
queue.remove();
for (int i = 0; i < this.nodes.get(u).size(); ++i)
{
int v = this.nodes.get(u).get(i);
if(!visited.get(v))
{
System.out.println(v);
visited.set(v, true);
queue.add(v);
}
}
}
}
}
Final Implementation
Python
class Graph:
N = 0
nodes = []
visited = []
def __init__(self):
self.N = N
self.nodes = []
self.visited = []
for u in range(N):
self.nodes.append([])
self.visited.append(False)
def addEdge(self, u, v):
self.nodes[u].append(v)
def BFS(self):
u = 0
queue = []
self.visited[u] = True
queue.append(u)
print(u)
while len(queue) > 0:
u = queue.pop(0)
for v in self.nodes[u]:
if(self.visited[v] == False):
self.visited[v] = True
queue.append(v)
print(v)
graph = Graph(5)
graph.addEdge(0, 1) # A => B
graph.addEdge(0, 2) # A => C
graph.addEdge(0, 3) # A => D
graph.addEdge(1, 0) # B => A
graph.addEdge(1, 3) # B => D
graph.addEdge(1, 4) # B => E
graph.addEdge(2, 0) # C => A
graph.addEdge(2, 3) # C => D
graph.addEdge(3, 0) # D => A
graph.addEdge(3, 1) # D => B
graph.addEdge(3, 2) # D => C
graph.addEdge(3, 4) # D => E
graph.addEdge(4, 1) # E => B
graph.addEdge(4, 3) # E => D
graph.BFS()
Java
import java.io.*;
import java.util.*;
public class Graph
{
private int N;
private ArrayList<ArrayList<Integer>> nodes;
private ArrayList<Boolean> visited;
public Graph(int n)
{
this.N = n;
this.nodes = new ArrayList<ArrayList<Integer>>();
this.visited = new ArrayList<Boolean>();
for (int i = 0; i < this.N; ++i)
{
this.nodes.add(new ArrayList<Integer>());
this.visited.add(false);
}
}
public void addEdge(int u, int v)
{
this.nodes.get(u).add(v);
}
public void BFS()
{
int u = 0;
Queue<Integer> queue = new LinkedList<>();
System.out.println(u);
visited.set(u, true);
queue.add(u);
while (queue.size() != 0)
{
u = queue.peek();
queue.remove();
for (int i = 0; i < this.nodes.get(u).size(); ++i)
{
int v = this.nodes.get(u).get(i);
if(!visited.get(v))
{
System.out.println(v);
visited.set(v, true);
queue.add(v);
}
}
}
}
public static void main(String[] args) {
Graph graph = new Graph(5);
graph.addEdge(0, 1); // A => B
graph.addEdge(0, 2); // A => C
graph.addEdge(0, 3); // A => D
graph.addEdge(1, 0); // B => A
graph.addEdge(1, 3); // B => D
graph.addEdge(1, 4); // B => E
graph.addEdge(2, 0); // C => A
graph.addEdge(2, 3); // C => D
graph.addEdge(3, 0); // D => A
graph.addEdge(3, 1); // D => B
graph.addEdge(3, 2); // D => C
graph.addEdge(3, 4); // D => E
graph.addEdge(4, 1); // E => B
graph.addEdge(4, 3); // E => D
graph.BFS();
}
}
Final Output
0
1
2
3
4
Time complexity
The time complexity of the algorithm will be same as the DFS which can be measured by computing the number of times a core statement of the code is been executing. The algorithm’s core statement would be iterating each node and mark it as “visited”. The method call will happen exactly once per node as we are not allowing the method to execute if the node is already visited. Hence the time taken is the same as the N (number of nodes).
Time Complexity = O(N)
We can write Traversal Algorithms in C++ or any other programming language as well. If feel you need help with java programming or looking for python programming help, contact us now and we will assist you in the best possible way.